KALAH VS SITTUYIN

Kalah, also called Kalaha or Mancala, is a game in the mancala family invented in the United States by William Julius Champion, Jr. in 1940. This game is sometimes also called "Kalahari", possibly by false etymology from the Kalahari desert in Namibia. As the most popular and commercially available variant of mancala in the West, Kalah is also sometimes referred to as Warri or Awari, although those names more properly refer to the game Oware. For most of its variations, Kalah is a solved game with a first-player win if both players play perfect games. The Pie rule can be used to balance the first-player's advantage. Mark Rawlings has written a computer program to extensively analyze both the "standard" version of Kalah and the "empty capture" version, which is the primary variant. The analysis was made possible by the creation of the largest endgame databases ever made for Kalah. They include the perfect play result of all 38,902,940,896 positions with 34 or fewer seeds. In 2015, for the first time ever, each of the initial moves for the standard version of Kalah(6,4) and Kalah(6,5) have been quantified: Kalah(6,4) is a proven win by 8 for the first player and Kalah(6,5) is a proven win by 10 for the first player. In addition, Kalah(6,6) with the standard rules has been proven to be at least a win by 4. Further analysis of Kalah(6,6) with the standard rules is ongoing. For the "empty capture" version, Geoffrey Irving and Jeroen Donkers (2000) proved that Kalah(6,4) is a win by 10 for the first player with perfect play, and Kalah(6,5) is a win by 12 for the first player with perfect play. Anders Carstensen (2011) proved that Kalah(6,6) was a win for the first player. Mark Rawlings (2015) has extended these "empty capture" results by fully quantifying the initial moves for Kalah(6,4), Kalah(6,5), and Kalah(6,6). With searches totaling 106 days and over 55 trillion nodes, he has proven that Kalah(6,6) is a win by 2 for the first player with perfect play. This was a surprising result, given that the "4-seed" and "5-seed" variations are wins by 10 and 12, respectively. Kalah(6,6) is extremely deep and complex when compared to the 4-seed and 5-seed variations, which can now be solved in a fraction of a second and less than a minute, respectively.

See statistics

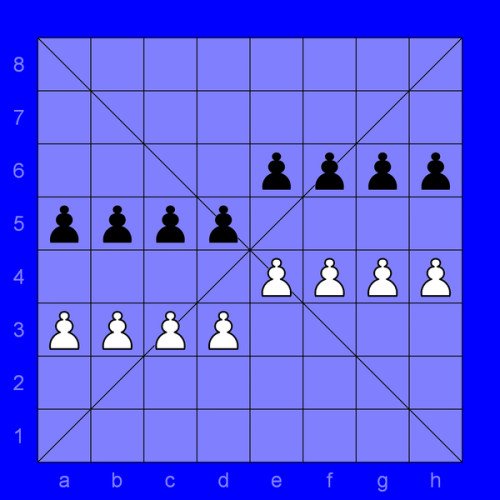
Sittuyin (Burmese: စစ်တုရင်), also known as Burmese chess, is a variant of chess that is a direct offspring of the Indian game of chaturanga which arrived in 8th century AD. Sit is the modern Burmese word for army or war ; the word sittuyin can be translated as representation of the four characteristics of army—chariot, elephant, cavalry and infantry. In its native land the game has been largely overshadowed by Western (international) chess, although it remains popular in the northwest regions. The sittuyin board consists of 64 squares, 8 rows and 8 columns, without alternating colors. It also consists of two diagonal lines across the board known as sit-ke-myin (general's lines). Only feudal lords (pawns) are on the board in the initial position. The game starts with the Red player (depicted here having white pieces), followed by the Black player, placing their other pieces arbitrarily on their own halves of the board (known as sit-tee or troops deployment): chariots can be put on any square on the back rank. In official tournaments, a small curtain is used on the middle of the board to prevent the players seeing each other's deployment during the sit-tee phase. One of the possible game openings is shown in the diagram. Feudal lords promote to general when they reach diagonal lines marked on the board. The promotion is possible only if that player's general has been captured. If the player has a feudal lord on a promotion square and his or her general is no longer on the board, the player can (if he or she wishes to) promote the feudal lord to general instead of making a move. A feudal lord which passes the promotion square cannot promote anymore.

See statistics