JANGGI VS KALAH

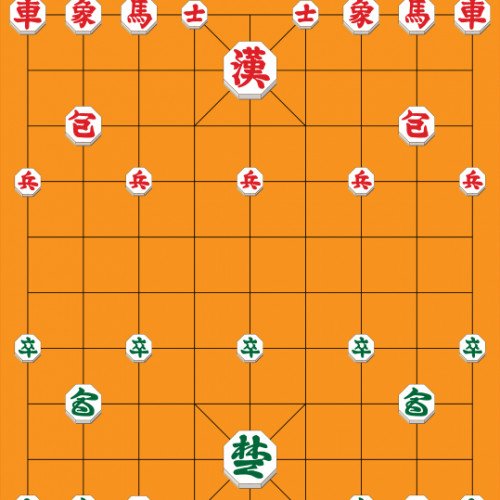
Janggi (including romanizations changgi and jangki), sometimes called Korean chess, is a strategy board game popular in Korea. The game was derived from xiangqi (Chinese chess) of China and is very similar to it, including the starting position of the pieces, and the 9×10 gameboard, but without the xiangqi "river" dividing the board horizontally in the middle. Janggi is played on a board nine lines wide by ten lines long. The game is sometimes fast paced due to the jumping cannons and the long-range elephants, but professional games most often last over 150 moves and so are typically slower than those of Western chess. In 2009, the first world janggi tournament was held in Harbin, Heilongjiang China. The board is composed of 90 intersections of 9 vertical files and 10 horizontal rows. The board has nearly the same layout as that used in xiangqi, except the janggi board has no "river" in the central row. The pieces consist of disks marked with identifying characters and are placed on the line intersections (as in xiangqi and Go in China). Janggi pieces are traditionally octagonal in shape, and differ in size according to their rank. The sides are Blue (or sometimes Green), which moves first, versus Red. Each side has a palace that is 3 lines by 3 lines (9 positions) in the centre of their side of the board against the back edge. The palace contains four diagonal lines extending outwards from the centre, forming an "X" shape.

See statistics

Kalah, also called Kalaha or Mancala, is a game in the mancala family invented in the United States by William Julius Champion, Jr. in 1940. This game is sometimes also called "Kalahari", possibly by false etymology from the Kalahari desert in Namibia. As the most popular and commercially available variant of mancala in the West, Kalah is also sometimes referred to as Warri or Awari, although those names more properly refer to the game Oware. For most of its variations, Kalah is a solved game with a first-player win if both players play perfect games. The Pie rule can be used to balance the first-player's advantage. Mark Rawlings has written a computer program to extensively analyze both the "standard" version of Kalah and the "empty capture" version, which is the primary variant. The analysis was made possible by the creation of the largest endgame databases ever made for Kalah. They include the perfect play result of all 38,902,940,896 positions with 34 or fewer seeds. In 2015, for the first time ever, each of the initial moves for the standard version of Kalah(6,4) and Kalah(6,5) have been quantified: Kalah(6,4) is a proven win by 8 for the first player and Kalah(6,5) is a proven win by 10 for the first player. In addition, Kalah(6,6) with the standard rules has been proven to be at least a win by 4. Further analysis of Kalah(6,6) with the standard rules is ongoing. For the "empty capture" version, Geoffrey Irving and Jeroen Donkers (2000) proved that Kalah(6,4) is a win by 10 for the first player with perfect play, and Kalah(6,5) is a win by 12 for the first player with perfect play. Anders Carstensen (2011) proved that Kalah(6,6) was a win for the first player. Mark Rawlings (2015) has extended these "empty capture" results by fully quantifying the initial moves for Kalah(6,4), Kalah(6,5), and Kalah(6,6). With searches totaling 106 days and over 55 trillion nodes, he has proven that Kalah(6,6) is a win by 2 for the first player with perfect play. This was a surprising result, given that the "4-seed" and "5-seed" variations are wins by 10 and 12, respectively. Kalah(6,6) is extremely deep and complex when compared to the 4-seed and 5-seed variations, which can now be solved in a fraction of a second and less than a minute, respectively.

See statistics