DIAMOND VS KALAH

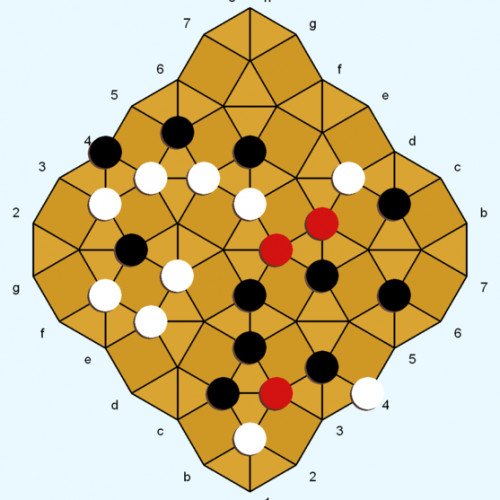
Diamond is a two-player abstract strategy board game invented by Larry Back. The invention was inspired by the game Kensington, which uses a similar board pattern and game objective. Rules for Diamond were conceived in 1985 and finalized in 1994. Diamond introduces a new board geometry and neutral pieces, with the aim of enhancing the game dynamic and lowering the potential for draws. Diamond was featured in the February 2013 issue of Games magazine. The Diamond gameboard consists of interlocking squares and triangles. White and Black each control 12 game pieces of their own color. Neutral pieces (red-colored in the diagrams) enter the game via captures. The pieces are played on the line intersections (called points, as in Go). White and black (but not red) pieces can move along straight lines to adjacent unoccupied points. A player wins by being the first to occupy all four corners (points) of a board square with their pieces. Capturing moves are possible in the Movement phase. If the points of a triangle contain exactly one white and one black piece, either player can capture the opponent piece by occupying the remaining open point ("cornering" the enemy piece on the triangle). The captured piece can be cornered on one triangle (see Example 1), or simultaneously cornered on two different triangles (Example 4). The captured piece is immediately removed from the game and replaced on its point by a neutral piece. If a move simultaneously corners two opponent pieces on two different triangles, then neither enemy piece is captured (Examples 2 and 3). A piece can move safely to a triangle point even if the other two points of the triangle are occupied by enemy pieces (Example 5).

See statistics

Kalah, also called Kalaha or Mancala, is a game in the mancala family invented in the United States by William Julius Champion, Jr. in 1940. This game is sometimes also called "Kalahari", possibly by false etymology from the Kalahari desert in Namibia. As the most popular and commercially available variant of mancala in the West, Kalah is also sometimes referred to as Warri or Awari, although those names more properly refer to the game Oware. For most of its variations, Kalah is a solved game with a first-player win if both players play perfect games. The Pie rule can be used to balance the first-player's advantage. Mark Rawlings has written a computer program to extensively analyze both the "standard" version of Kalah and the "empty capture" version, which is the primary variant. The analysis was made possible by the creation of the largest endgame databases ever made for Kalah. They include the perfect play result of all 38,902,940,896 positions with 34 or fewer seeds. In 2015, for the first time ever, each of the initial moves for the standard version of Kalah(6,4) and Kalah(6,5) have been quantified: Kalah(6,4) is a proven win by 8 for the first player and Kalah(6,5) is a proven win by 10 for the first player. In addition, Kalah(6,6) with the standard rules has been proven to be at least a win by 4. Further analysis of Kalah(6,6) with the standard rules is ongoing. For the "empty capture" version, Geoffrey Irving and Jeroen Donkers (2000) proved that Kalah(6,4) is a win by 10 for the first player with perfect play, and Kalah(6,5) is a win by 12 for the first player with perfect play. Anders Carstensen (2011) proved that Kalah(6,6) was a win for the first player. Mark Rawlings (2015) has extended these "empty capture" results by fully quantifying the initial moves for Kalah(6,4), Kalah(6,5), and Kalah(6,6). With searches totaling 106 days and over 55 trillion nodes, he has proven that Kalah(6,6) is a win by 2 for the first player with perfect play. This was a surprising result, given that the "4-seed" and "5-seed" variations are wins by 10 and 12, respectively. Kalah(6,6) is extremely deep and complex when compared to the 4-seed and 5-seed variations, which can now be solved in a fraction of a second and less than a minute, respectively.

See statistics