ASALTO VS RITHMOMACHY

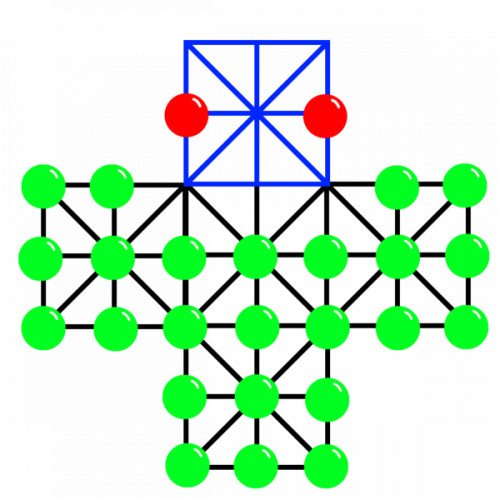
Asalto, also known as the Assault Game, German Tactics or Officers and Sepoys, is a board game for two players in which one player, playing as the officers, attempts to defend a fortress from their opponent's invading rebels. The game is a variant on the Fox and Geese theme, and is commonly played in Germany, France, and England. Asalto is an asymmetric game in which the players take on two very different roles: the rebels and the officers. The rebels' objective is to capture the two officers, surround them so that they cannot move, or occupy all of the points within the "fortress". The officers' objective is to capture enough rebels that these tasks become impossible. Asalto is played on a grid of 33 intersection points in the shape of a cross, with a specially denoted arm known as the fortress at the top of the board. The total number of pieces in an Asalto game is 26, composed of 24 rebels and two officers. Before play begins, the rebels are arranged so that they sit on the 24 intersection points outside the fortress, while the officers may be arranged at the player's discretion inside the fortress. The game begins once the rebel player takes the first turn.

See statistics

Rithmomachy (or Rithmomachia, also Arithmomachia, Rythmomachy, Rhythmomachy, or several other variants; sometimes known as The Philosophers' Game) is a highly complex, early European mathematical board game. The earliest known description of it dates from the eleventh century. A literal translation of the name is "The Battle of the Numbers". The game is much like chess, except most methods of capture depend on the numbers inscribed on each piece. It has been argued that between the twelfth and sixteenth centuries, "rithmomachia served as a practical exemplar for teaching the contemplative values of Boethian mathematical philosophy, which emphasized the natural harmony and perfection of number and proportion. The game, Moyer argues, was used both as a mnemonic drill for the study of Boethian number theory and, more importantly, as a vehicle for moral education, by reminding players of the mathematical harmony of creation." Very little, if anything, is known about the origin of the game. Medieval writers attributed it to Pythagoras, but no trace of it has been discovered in Greek literature, and the earliest mention of it is from the time of Hermannus Contractus (1013–1054). The name, which appears in a variety of forms, points to a Greek origin, the more so because Greek was little known at the time when the game first appeared in literature. Based upon the Greek theory of numbers, and having a Greek name, it is still speculated by some that the game originated in Greek civilization, perhaps in the later schools of Byzantium or Alexandria. The first written evidence of Rithmomachia dates to around 1030, when a monk named Asilo created a game that illustrated the number theory of Boëthius' De institutione arithmetica, for the students of monastery schools. The rules of the game were improved shortly thereafter by another monk, Hermannus Contractus from Reichenau, and in the school of Liège. In the following centuries, Rithmomachia spread quickly through schools and monasteries in the southern parts of Germany and France. It was used mainly as a teaching aid, but gradually intellectuals started to play it for pleasure. In the 13th century Rithmomachia came to England, where famous mathematician Thomas Bradwardine wrote a text about it. Even Roger Bacon recommended Rithmomachia to his students, while Sir Thomas More let the inhabitants of the fictitious Utopia play it for recreation. The game was well enough known as to justify printed treatises in Latin, French, Italian, and German, in the sixteenth century, and to have public advertisements of the sale of the board and pieces under the shadow of the old Sorbonne.

See statistics