ASALTO VS KALAH

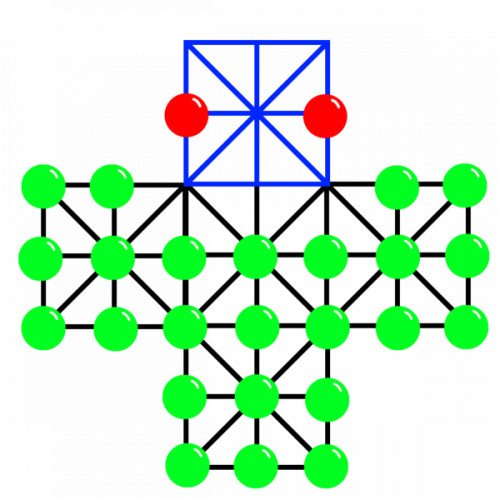
Asalto, also known as the Assault Game, German Tactics or Officers and Sepoys, is a board game for two players in which one player, playing as the officers, attempts to defend a fortress from their opponent's invading rebels. The game is a variant on the Fox and Geese theme, and is commonly played in Germany, France, and England. Asalto is an asymmetric game in which the players take on two very different roles: the rebels and the officers. The rebels' objective is to capture the two officers, surround them so that they cannot move, or occupy all of the points within the "fortress". The officers' objective is to capture enough rebels that these tasks become impossible. Asalto is played on a grid of 33 intersection points in the shape of a cross, with a specially denoted arm known as the fortress at the top of the board. The total number of pieces in an Asalto game is 26, composed of 24 rebels and two officers. Before play begins, the rebels are arranged so that they sit on the 24 intersection points outside the fortress, while the officers may be arranged at the player's discretion inside the fortress. The game begins once the rebel player takes the first turn.

See statistics

Kalah, also called Kalaha or Mancala, is a game in the mancala family invented in the United States by William Julius Champion, Jr. in 1940. This game is sometimes also called "Kalahari", possibly by false etymology from the Kalahari desert in Namibia. As the most popular and commercially available variant of mancala in the West, Kalah is also sometimes referred to as Warri or Awari, although those names more properly refer to the game Oware. For most of its variations, Kalah is a solved game with a first-player win if both players play perfect games. The Pie rule can be used to balance the first-player's advantage. Mark Rawlings has written a computer program to extensively analyze both the "standard" version of Kalah and the "empty capture" version, which is the primary variant. The analysis was made possible by the creation of the largest endgame databases ever made for Kalah. They include the perfect play result of all 38,902,940,896 positions with 34 or fewer seeds. In 2015, for the first time ever, each of the initial moves for the standard version of Kalah(6,4) and Kalah(6,5) have been quantified: Kalah(6,4) is a proven win by 8 for the first player and Kalah(6,5) is a proven win by 10 for the first player. In addition, Kalah(6,6) with the standard rules has been proven to be at least a win by 4. Further analysis of Kalah(6,6) with the standard rules is ongoing. For the "empty capture" version, Geoffrey Irving and Jeroen Donkers (2000) proved that Kalah(6,4) is a win by 10 for the first player with perfect play, and Kalah(6,5) is a win by 12 for the first player with perfect play. Anders Carstensen (2011) proved that Kalah(6,6) was a win for the first player. Mark Rawlings (2015) has extended these "empty capture" results by fully quantifying the initial moves for Kalah(6,4), Kalah(6,5), and Kalah(6,6). With searches totaling 106 days and over 55 trillion nodes, he has proven that Kalah(6,6) is a win by 2 for the first player with perfect play. This was a surprising result, given that the "4-seed" and "5-seed" variations are wins by 10 and 12, respectively. Kalah(6,6) is extremely deep and complex when compared to the 4-seed and 5-seed variations, which can now be solved in a fraction of a second and less than a minute, respectively.

See statistics