Agon (or Queen's Guards or Royal Guards) is an strategy game invented by Anthony Peacock of London, and first published in 1842. It is a two player ga...
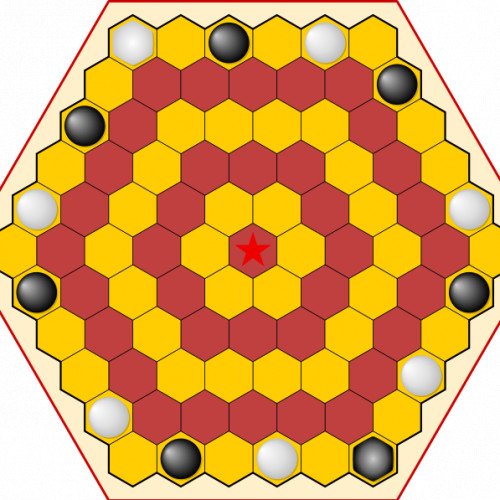
Agon (or Queen's Guards or Royal Guards) is an strategy game invented by Anthony Peacock of London, and first published in 1842. It is a two player game played on a 6×6×6 hexagonal gameboard, and is notable for being the oldest known board game played on a board of hexagonal cells.
Each player has one queen and six guards. Players determine who moves first, then turns alternate. On each turn, a player moves one of his pieces. The object of the game is to be first to maneuver one's queen to the central hex (the throne) at the center of the board, and surround her with all six of her guards.
The gameboard may be thought of as a series of concentric rings of hex cells (highlighted by rings of alternating colors). Pieces move one step at a time to an adjacent cell, either sideways in the same ring, or towards the throne to the next ring. The cell moved to must be vacant. Only the queen may move to the throne.
VS
RITHMOMACHY
Rithmomachy (or Rithmomachia, also Arithmomachia, Rythmomachy, Rhythmomachy, or several other variants; sometimes known as The Philosophers' Game) is...
Rithmomachy (or Rithmomachia, also Arithmomachia, Rythmomachy, Rhythmomachy, or several other variants; sometimes known as The Philosophers' Game) is a highly complex, early European mathematical board game. The earliest known description of it dates from the eleventh century. A literal translation of the name is "The Battle of the Numbers". The game is much like chess, except most methods of capture depend on the numbers inscribed on each piece.
It has been argued that between the twelfth and sixteenth centuries, "rithmomachia served as a practical exemplar for teaching the contemplative values of Boethian mathematical philosophy, which emphasized the natural harmony and perfection of number and proportion. The game, Moyer argues, was used both as a mnemonic drill for the study of Boethian number theory and, more importantly, as a vehicle for moral education, by reminding players of the mathematical harmony of creation."
Very little, if anything, is known about the origin of the game. Medieval writers attributed it to Pythagoras, but no trace of it has been discovered in Greek literature, and the earliest mention of it is from the time of Hermannus Contractus (1013–1054).
The name, which appears in a variety of forms, points to a Greek origin, the more so because Greek was little known at the time when the game first appeared in literature. Based upon the Greek theory of numbers, and having a Greek name, it is still speculated by some that the game originated in Greek civilization, perhaps in the later schools of Byzantium or Alexandria.
The first written evidence of Rithmomachia dates to around 1030, when a monk named Asilo created a game that illustrated the number theory of Boëthius' De institutione arithmetica, for the students of monastery schools. The rules of the game were improved shortly thereafter by another monk, Hermannus Contractus from Reichenau, and in the school of Liège. In the following centuries, Rithmomachia spread quickly through schools and monasteries in the southern parts of Germany and France. It was used mainly as a teaching aid, but gradually intellectuals started to play it for pleasure. In the 13th century Rithmomachia came to England, where famous mathematician Thomas Bradwardine wrote a text about it. Even Roger Bacon recommended Rithmomachia to his students, while Sir Thomas More let the inhabitants of the fictitious Utopia play it for recreation.
The game was well enough known as to justify printed treatises in Latin, French, Italian, and German, in the sixteenth century, and to have public advertisements of the sale of the board and pieces under the shadow of the old Sorbonne.
Comments (0)
No comments yet. Be the first to share your thoughts!